一、前言

相信很多人都已经忘记或者没用过这个关键字，或者基本上都是初学时用过，然后就未曾使用。

笔者也是在阅读以前大学写的纸质笔记时，这才回忆起这个关键字。

二、简介

strictfp 全称：Strict Floating-Point（严格浮点）

使用方式：可以将类、接口、方法声明为 strictfp，但不允许对接口中的方法以及构造函数声明。（strictfp 影响范围内的方法都将是严格浮点，例如若一个类被声明为 strictfp，则类内部的所有方法都是严格浮点的）

作用：使得浮点运算严格按照 IEEE-754 规范，不会因为硬件平台的不同而导致执行结果不一致。

二、使用示例

其实，你可以在 java.lang.StrictMath.java 中看到大量使用 strictfp 的方法（Java 17 开始这里就不用 strictfp 了，原因见下文 JEP 306）。

public static strictfp double toRadians(double angdeg) {
    // Do not delegate to Math.toRadians(angdeg) because
    // this method has the strictfp modifier.
    return angdeg / 180.0 * PI;
}

三、更多背景知识

3.1 JEP 306

详见：JEP 306: Restore Always-Strict Floating-Point Semantics

以下内容均来自上面的 JEP 306：

strictfp 在 Java SE 1.2 引入，在 Java SE 17 开始没啥用了（因为都是严格模式了）
（以前为什么有，现在又为什么不需要）在 1990 年代后期，改变平台默认浮点语义的动力源于原始 Java 语言和 JVM 语义之间的不良交互，以及流行的 x86 架构的 x87 浮点协处理器指令集的一些不幸特性。在所有情况下匹配精确的浮点语义（包括次正态操作数和结果）都需要大量额外的指令开销。在没有溢出或下溢的情况下匹配结果可以用更少的开销来实现，这大致是 Java SE 1.2 中引入的修订后的默认浮点语义所允许的。但是，从2001年左右开始，在奔腾4及更高版本的处理器中提供的SSE2（Streaming SIMD Extensions 2）扩展可以以简单的方式支持严格的JVM浮点运算，而不会产生不必要的开销。由于 Intel 和 AMD 长期以来一直支持 SSE2 和更高版本的扩展，这些扩展允许自然支持严格的浮点语义，因此不再存在使用不同于严格语义的默认浮点语义的技术动机。（默认浮点语义更宽松，会因为计算机二进制表示固有的浮点精度差异问题导致部分情况下不同平台上的计算结果产生细微差异）
使浮点运算始终严格，而不是同时具有严格的浮点语义（strictfp）和略有不同的默认浮点语义。这会将原始浮点语义恢复到语言和 VM，与在 Java SE 1.2 中引入严格和默认浮点模式之前的语义相匹配。（Java SE 1.2 之前只有严格模式）

3.2 《Java核心技术·卷Ⅰ：基础知识（原书第10版）》的 3.5运算符

注释：可移植性是Java语言的设计目标之一。无论在哪个虚拟机上运行，同一运算应该得到同样的结果。对于浮点数的算术运算，实现这样的可移植性是相当困难的。double类型使用64位存储一个数值，而有些处理器使用80位浮点寄存器。这些寄存器增加了中间过程的计算精度。例如，以下运算：

double w = x * y / z;

很多Intel处理器计算 x * y，并且将结果存储在80位的寄存器中，再除以 z 并将结果截断为64位。这样可以得到一个更加精确的计算结果，并且还能够避免产生指数溢出。但是，这个结果可能与始终在64位机器上计算的结果不一样。因此，Java虚拟机的最初规范规定所有的中间计算都必须进行截断。这种行为遭到了数值计算团体的反对。截断计算不仅可能导致溢出，而且由于截断操作需要消耗时间，所以在计算速度上实际上要比精确计算慢。为此，Java程序设计语言承认了最优性能与理想结果之间存在的冲突，并给予了改进。在默认情况下，虚拟机设计者允许对中间计算结果采用扩展的精度。但是，对于使用strictfp关键字标记的方法必须使用严格的浮点计算来生成可再生的结果。例如，可以把main方法标记为

public static strictfp void main(String[] args)

于是，在main方法中的所有指令都将使用严格的浮点计算。如果将一个类标记为strictfp，这个类中的所有方法都要使用严格的浮点计算。

实际的计算方式将取决于Intel处理器的行为。在默认情况下，中间结果允许使用扩展的指数，但不允许使用扩展的尾数（Intel芯片在截断尾数时并不损失性能）。因此，这两种方式的区别仅仅在于采用默认的方式不会产生溢出，而采用严格的计算有可能产生溢出。

如果没有仔细阅读这个注释，也没有什么关系。对大多数程序来说，浮点溢出不属于大问题。

四、关于浮点精度问题

其实，strictfp 只是解决了跨平台的计算结果不一致的问题。IEEE-754 规范本身定义的浮点运算，始终是对浮点运算精度问题无可奈何，特别是 0.1 这样的值。

举个例子：0.1 + 0.2 =0.3

下图是程序跑的结果：

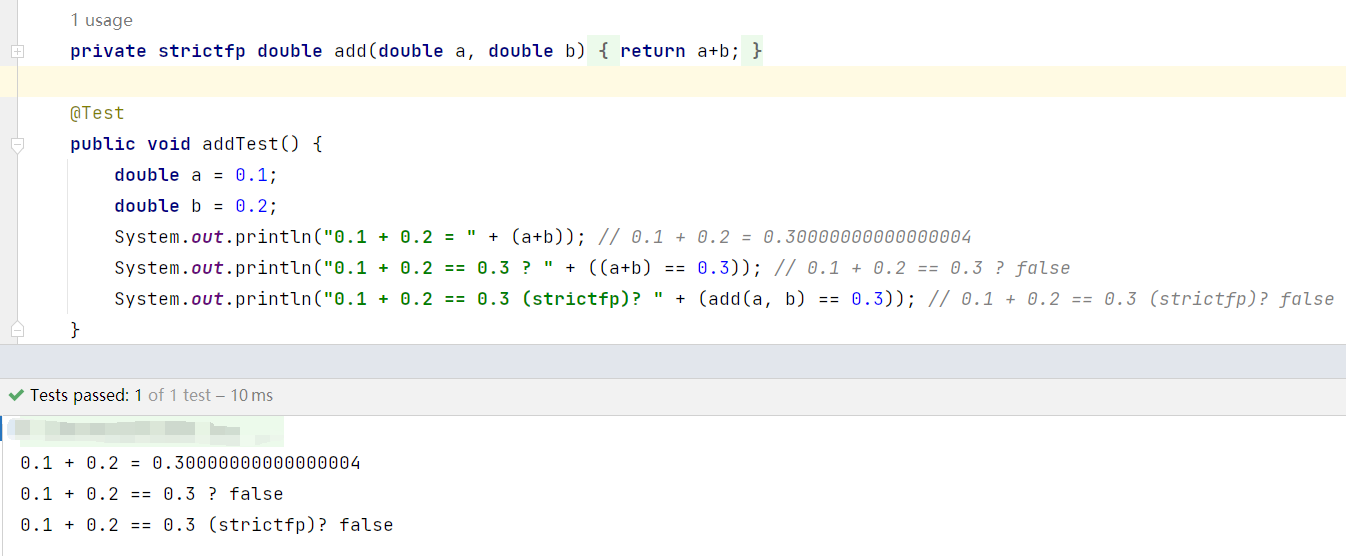
如果是对计算结果的精确度很敏感，比如金融交易计算，实际上就不应该用 float 或者 double 这类浮点来计算，而应该用 BigDecimal 或者转成整数来计算。

注意：需要先转换成字符串形式，再利用 BigDecimal 初始化，直接利用 BigDecimal 的浮点数构造方法可能引入不确定的值，具体在构造方法 BigDecimal(double val) 的注释中就有说明。

下图为 BigDecimal 使用示例：

Menu

Share

Java 关键字strictfp